Все детали можно рассматривать как геометрические объекты. При обработке детали инструмент и заготовка перемещаются относительно друг друга по определенной траектории. В управляющей программе по обработке детали описывается движение определенной точки инструмента – его центра, расположение которого зависит от вида инструмента.
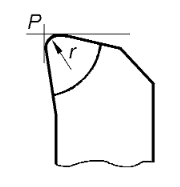
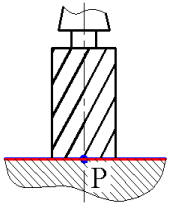
Например, для резцов – это центр дуги окружности при вершине, для сверла, зенкера, концевой цилиндрической фрезы – это точка пересечения оси и торца инструмента.
Для обработки детали траектория движения центра инструмента должна быть непрерывной.
Траекторию инструмента представляют состоящей из отдельных, последовательно переходящих друг в друга участков. Эти участки могут быть или участками контура детали, или участками эквидистанты.
Эквидистанта - это геометрическое место точек, равноудаленных от какой-либо линии и лежащих по одну сторону от нее. Она бывает внешней и внутренней. Например, траектория перемещения фрезы при обработке отверстия будет представлять собой внутреннюю эквидистанту, а при обработке наружного контура детали – внешнюю эквидитанту.
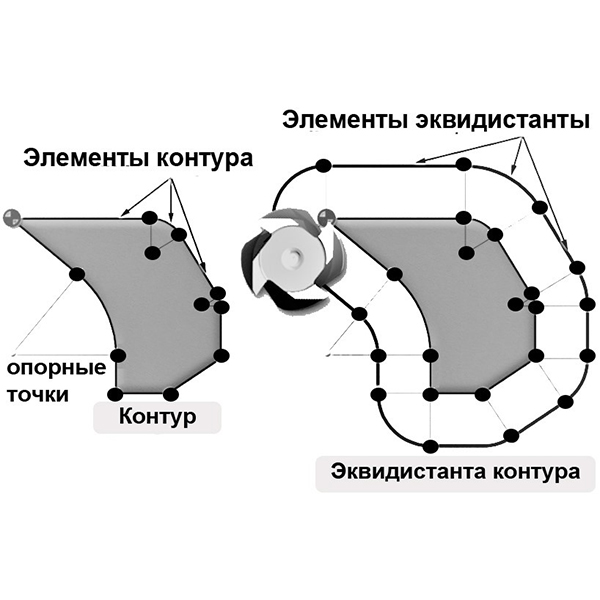
Траектория движения инструмента состоит из простых элементов. В большинстве случаев такими элементами являются отрезки прямых и дуги окружностей, кривые второго и высших порядков. Точки пересечения простых элементов или перехода одного элемента в другой называются опорными точками контура. Они задаются координатами или в пространстве или на плоскости. На траектории движения центра инструмента могут быть назначены также технологические опорные точки (т. е. где происходит изменение режимов обработки, временного останова с указанием времени останова).
Начальный этап представления траектории обработки детали связан прежде всего с получением координат опорных точек траектории.
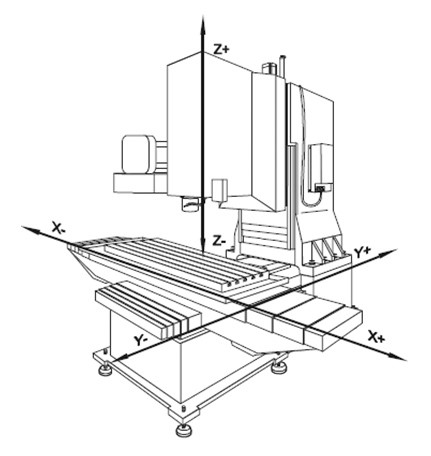
Для станков с ЧПУ принята единая система координат, рекомендуемая Международной организацией по стандартизации (ISO), – прямоугольная система координат. Число координатных осей, их расположение в пространстве и начало отсчета (нулевая точка станка) устанавливаются производителем станка и не подлежит изменению пользователем.
Система координат станка является основной расчетной системой для ЧПУ, в которой определяются предельные перемещения, начальные и текущие положения исполнительных органов станка. Для удобства программирования процесса обработки в станках с ЧПУ принято координатные оси всегда ориентировать параллельно направляющим станка.
В зависимости от типа станка расположение осей координат в пространстве может быть различным, но существуют следующие общие правила:
1. Ось Z всегда совмещена с осью вращения шпинделя. Ее положительное направление всегда совпадает с направлением перемещения от устройства для крепления заготовки к режущему инструменту (направление отвода инструмента от заготовки).
2. Если в системе координат станка имеется хотя бы одна ось, расположенная горизонтально и не совпадающая с осью вращения шпинделя, то это будет обязательно ось X.
3. На станках с вращающейся заготовкой (токарные) движение по оси X направлено параллельно поперечным направляющим по радиусу заготовки. Положительное движение по оси X происходит, когда инструмент, установленный в главном резцедержателе поперечных салазок, отходит от оси вращения заготовки
4. На станках с вращающимся инструментом (фрезерные, сверлильные) при горизонтальном расположении оси Z положительное перемещение по оси X направлено вправо, если смотреть от основного инструменталь-ного шпинделя в сторону изделия. При вертикальном расположении оси Z положительное перемещение по оси X вправо для одностоечных станков, а для двухстоечных – от основного инструментального шпинделя на левую стойку.
5. Положительное направление оси Y определяется по одному из следующих правил:
– Смотря вдоль оси Z в положительном направлении, мысленно повернуть ось X на 90° по часовой стрелке вокруг оси Z.
– Правило правой руки: если мысленно поместить ладонь правой руки в начало координат таким образом, чтобы ось Z выходила из ладони перпендикулярно ей, а отогнутый под углом 90° к ладони большой палец показывал положительное направление оси X, то указательный палец будет показывать положительное направление оси Y.
В станках с ЧПУ наиболее часто используются системы координат двух видов:
- прямоугольная.
- полярная.
Прямоугольная система координат
Прямоугольная система координат является наиболее распространенной системой координат для станков с ЧПУ. Она содержит либо две оси координат (двухмерная система)
- для определения положения точек на плоскости, либо три оси (трехмерная система) - для определения положения точек в пространстве.
Для прямоугольной системы координат характерны следующие признаки:
- координатные оси располагаются взаимно перпендикулярно;
- координатные оси имеют общую точку пересечения (начало отсчета координат);
- координатные оси имеют одинаковый геометрический масштаб.
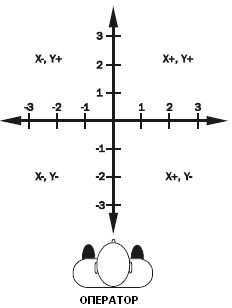
В прямоугольной системе координат на плоскости положение всех точек, лежащих на данной плоскости, описывается двумя координатами. На рисунке изображена такая система координат с осями координат X и Y. Расстояние до оси Y определяется как координата X, а расстояние до оси X как координата Y. Значения координат точек на плоскости могут иметь как положительные, так и отрицательные значения. Данная система координат широко применяется в токарных станках с ЧПУ и при обработке листовых материалов.
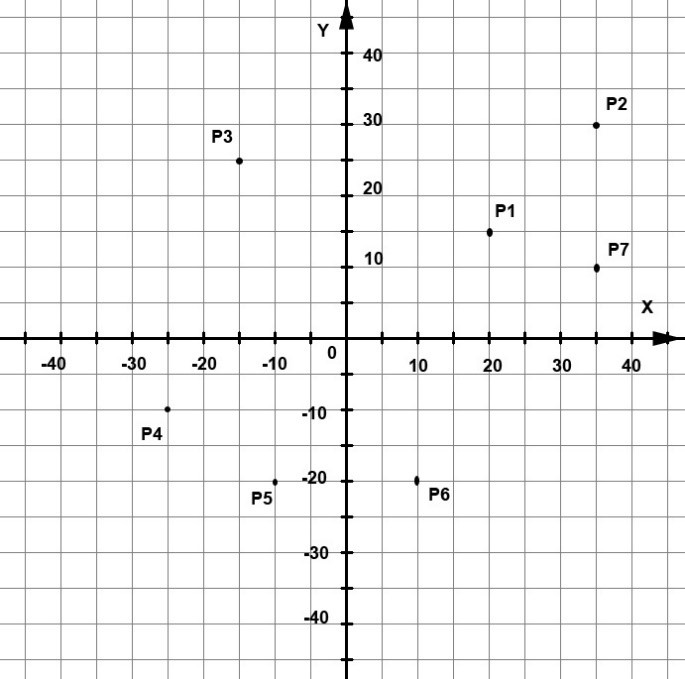
Пример обозначений координат указанных на рисунке точек:
Р1: Х=20, Y=15
P2: X=35, Y=30
P3: X=-15, Y=25
P4: X=-25, Y=-10
P5: X=-10, Y=-20
P6: X=10, Y=-20
P7: X=35, Y=10
С помощью пространственной прямоугольной системы координат описывается положение любых точек в геометрическом пространстве. Для определения положения любой точки в пространстве необходимо знать ее координаты по трем осям - X, Y и Z.. Как и в случае с плоской системой координат, значения координат точек в пространстве могут иметь как положительные, так и отрицательные значения. Данная система координат позволяет описывать все точки рабочего пространства станка независимо от расположения заготовки и применяется во фрезерных, сверлильных и расточных станках с ЧПУ.
Если обрабатываемый контур представляет собой ломаную линию, то с помощью прямоугольной системы координат можно легко задать все характерные точки его профиля. Однако ситуация меняется, если необходимо, например, выполнить на плоскости сверление группы отверстий, расположенных по окружности (см. рис. 1.4). Если для отверстия 1 координаты расположения его оси в прямоугольной системе координат можно рассчитать достаточно просто, то расчет расположения осей для всех других отверстий будет гораздо более трудоемким.
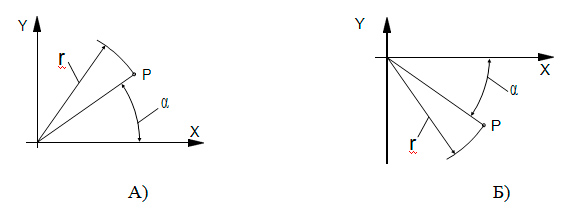
В этом случае вычисления удобнее выполнять в полярной системе координат. В полярной системе координат положение точки на плоскости определяется расстоянием (радиусом) r от точки до начала координат и углом α между определенной осью координат и радиусом, проведенным в точку из начала координат. Как правило, в полярной системе координат на плоскости XY угол α указывается от оси X. Угол α может иметь как положительное, так и отрицательное значение. Положительное значение – если он отложен в направлении противоположном движению часовой стрелки от области положительных значений координат по оси X (рис. 1.5–А); отрицательное значение – если он отложен в направлении по ходу движения часовой стрелки от области положительных значений координат по оси X (рис. 1.5–Б).
Это наиболее общий тип позиционирования.
Более распространенным является способ отсчета перемещений в абсолютной системе координат.
При абсолютном позиционировании все координаты задаются по отношению к началу координат, фиксированной нулевой точке, являющейся нулём детали.
Основные преимущества использования абсолютной системы координат:
Расчеты для определения координат требуют менее высокой квалификации работника из-за простоты;
- Единое начало координат позволяет отслеживать все перемещения режущего инструмента
- Изменения в перемещении, например, при обнаружении ошибки в координате опорной точки, не влияет на последующие перемещения по другим опорным точкам.
- погрешности изготовления и измерения, лежащие в пределах допустимых, не накапливаются (не суммируются).
При указании абсолютных размеров эти значения всегда относятся к нулевой точке детали.
Примеры:
А) токарная обработка
Б) фрезерная обработка
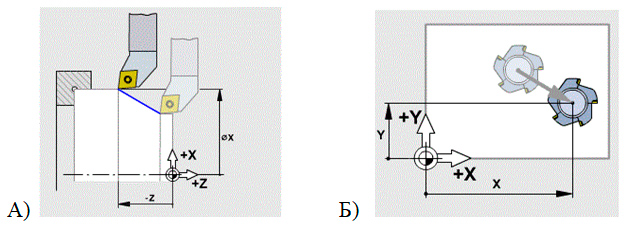
Особенность. При определении координаты по оси Х в абсолютной системе координат указывается диаметр.
При относительном позиционировании положение задаётся по отношению к предыдущей позиции инструмента. Координата следующей опорной точки вводится в единицах расстояния и направления относительно последней точки, а не нуля станка. Таким образом, при относительном позиционировании, текущая позиция является нулевой точкой для следующего перемещения.
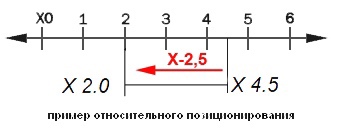
Пример. Обратите внимание, что перемещение по шкале от X 4.5 до X 2.0 является относительным перемещение X–2.5 хотя инструмент при этом остаётся в положительном направлении числовой прямой. Т.е., перемещение задаётся относительно последней позиции инструмента, а не нулевой точки детали. Знаки «+» и «–» определяют направление перемещения, а не местоположение координаты относительно нуля.
Необходимо помнить, что при абсолютном позиционировании мы рассматриваем координату и направление перемещения относительно нулевой точки детали, а при относительном — от последней позиции инструмента.
Абсолютное позиционирование является наиболее употребительным при программировании обработки деталей. Однако относительное позиционирование может облегчить создание программы в определённых случаях. Отличным примером этого может служить написание подпрограмм. Если вы имеете шесть одинаковых карманов, вы можете облегчить процесс программирования, написав подпрограмму обработки одного кармана в приращениях и вызвать её шесть раз для каждого кармана, задавая только начальную точку обработки.
Для вычисления неизвестных координат характерных точек наиболее часто используются геометрические свойства плоских треугольников и геометрические соотношения углов, образующихся при пересечении двух прямых.
Основные элементы треугольника
Треугольником на плоскости называется фигура, которая состоит из трех точек, лежащих в одной плоскости и не лежащих на одной прямой, и трех отрезков прямой линии, попарно соединяющих эти точки. В геометрии точки называются вершинами треугольника, а отрезки его сторонами. Обозначать треугольник в тексте или на чертеже принято с помощью букв, соответствующих его вершинам.
При составлении управляющих программ для станков с ЧПУ для описания треугольника используются все его основные элементы – вершины, углы и стороны, характерные обозначения которых представлены на рисунке 1.
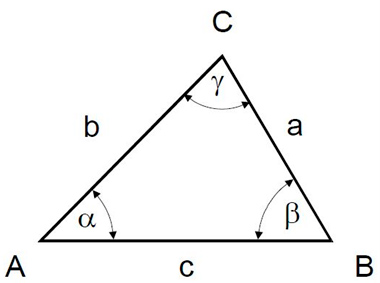
1.1.2. Углы треугольника
Существуют различные классификации треугольников. Для составления управляющих программ наиболее важно различать треугольники по углам. По этому признаку треугольники классифицируются на остроугольные, тупоугольные и прямоугольные (рисунок 2).
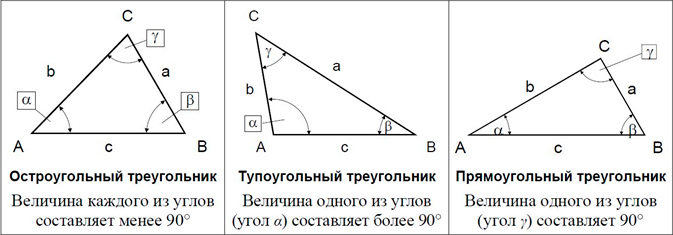
При вычислении координат для управляющей программы чаще всего используется следующая теорема о треугольниках: в любом треугольнике сумма всех узлов всегда равна 180°.
α + β + γ = 180°
Зная величины двух углов треугольника, не представляет труда по этой зависимости вычислить неизвестный третий угол.
1.1.3. Прямоугольный треугольник
Прямоугольный треугольник (рисунок 3) имеет особое значение для расчетов координат, поскольку существует строгая математическая зависимость между величинами его сторон. Для каждой стороны прямоугольного треугольника в аналитической геометрии существует свое название.
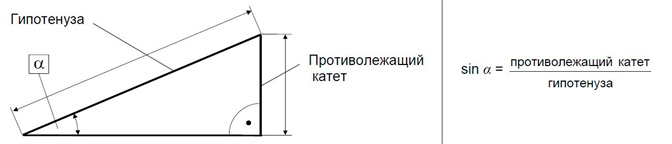
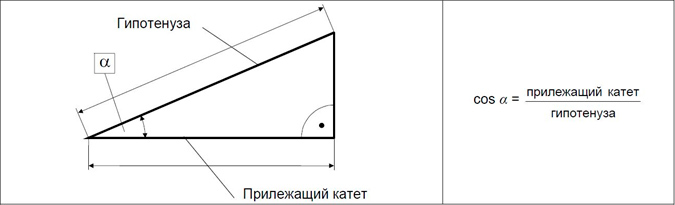
Гипотенузой называется сторона, противолежащая прямому углу.
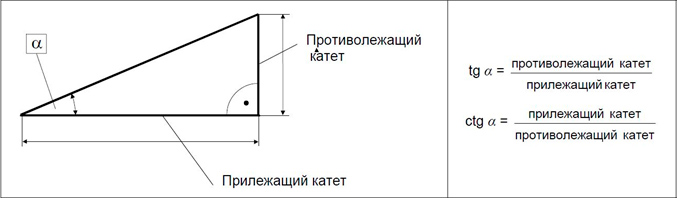
Катетами называются стороны, образующие прямой угол, при этом:
- Катет, противолежащий углу α, называется противолежащим катетом.
- Катет, являющийся одной из сторон угла α, называется прилежащим катетом.
Прямой угол прямоугольного треугольника на чертеже обозначается дугой с точкой внутри нее или прямоугольником, соответствующая вершина которого совпадает с вершиной прямого угла треугольника.
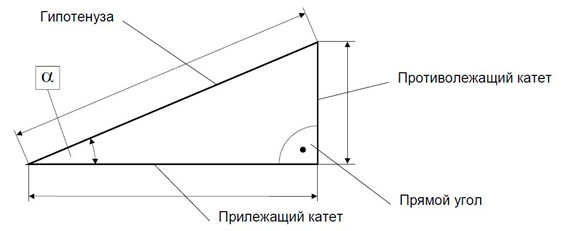
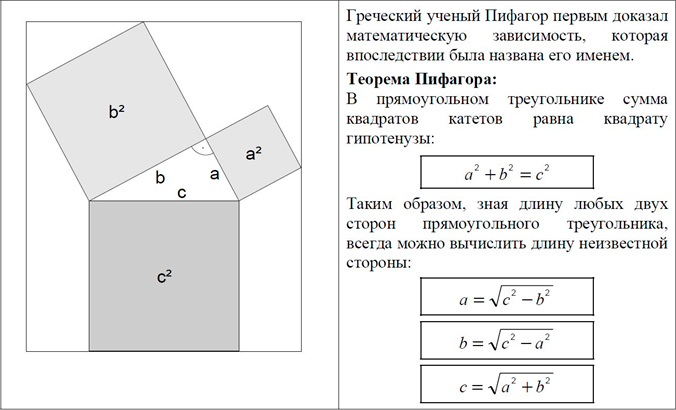
Для прямоугольного треугольника характерна однозначная математическая связь между его сторонами, всегда позволяющая вычислить длину одной стороны по длинам двух других сторон. Эта зависимость известна как теорема Пифагора (рисунок4).
1.1.4. Тригонометрические функции
Тригонометрические функции описывают математические зависимости между углами и сторонами прямоугольного треугольника. Используя тригонометрические функции, можно вычислить неизвестную длину одной из сторон при неизвестных значениях длины другой стороны и одного из острых углов. В зависимости от того, какая сторона и какой острый угол известны, а также от того, длину какой из двух неизвестных сторон требуется найти, в расчетах используются функции синуса sin (рисунок 5), косинуса cos (рисунок 6), тангенса tg или котангенса ctg (рисунок 7).
Для вычисления неизвестной стороны прямоугольного треугольника следует преобразовать приведенные на рисунках 5-7 соотношения таким образом, чтобы неизвестная величина оказалась в левой части, а известные - в правой части уравнения.
При работе на станке с ЧПУ одновременно в работе находятся несколько систем координат, в которых работают различные механизмы станка.
1. Координатная система станка.
Эта система является главной расчетной системой, в которой определяют все положения и перемещения исполнительных органов станка. Ее расположение зависит от группы и типа станка. Точка, представляющая собой начало отсчета координатной системы станка, называется нулем станка или нулевой точкой станка.
2. Координатная система детали.
Эта система - главная система для программирования обработки. Ее выбирает (назначает) программист (технолог) после анализа чертежа, эскиза и технологической документации. Точка начала отсчета координатной системы детали называется нулем детали или нулевой точкой детали.
3. Координатная система инструмента.
Эта система предназначена для задания положения режущей части инструмента относительно державки в момент обработки. Началом отсчета является точка, от которой начинается запрограммированное перемещение рабочего инструмента, которая называется нулем инструмента.
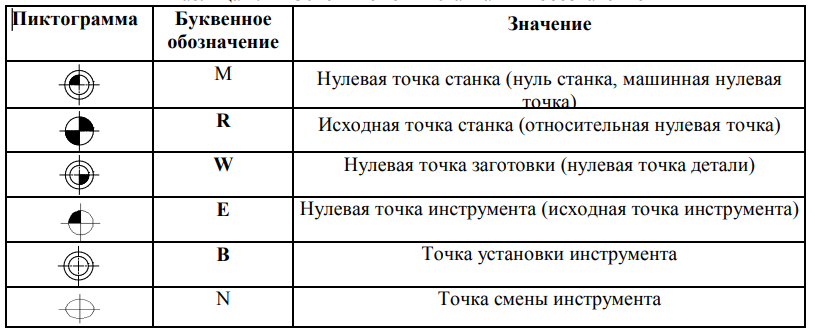
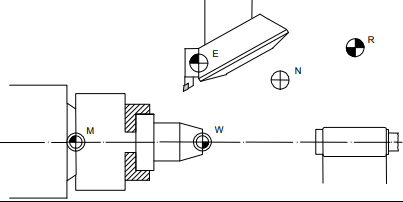
Нулевые точки систем, которые используются в работе, обозначаются пиктограммами и буквами латинского алфавита. при работе на станках с ЧПУ, как правило, имеют специальные обозначения, с помощью которых указывается их расположение на пульте станка или на эскизах технологической документации. Эти обозначения обычно состоят из пиктограммы и прописной буквы латинского алфавита. Типовые обозначения представлены в таблице. Пример расположения нулевых точек на токарном станке представлен на рисунке.